What's an L-System?
An L-System, short for Lindenmayer System, is a string re-writing algorithm that can be used to produce strings that can then be processed to generate geometry. In a nutshell, you take a starting string, called an axiom, and a list of rewrite rules, called productions, which you use to rewrite the axiom into a new string, which can than be rewritten again and again, ad infinitum.
An example:
Axiom: A Productions: A → AB B → A
0: A
1: AB
2: ABA
3: ABAAB
4: ABAABABA
5: ABAABABAABAAB
6: ABAABABAABAABABAABABA
What's Turtle Graphics?
As mentioned above, you can take a string generated from an L-System and use it to generate geometry. The most popular method of doing this is by using a cursor whose state is manipulated by the symbols in the string produced by the L-System. For fun, we can imagine that this cursor is a turtle.
The turtle has three attributes: a location (initialized to the origin), an orientation (initialized to the X unit vector), and a pen. It can be commanded relative to the current state of these attributes: rather than saying "draw a line from (0, 0) to (3, 0)", instead you would say "move forward 3 units while drawing". If you wanted to make a square with end points (0, 0), (3, 0), (3, 3), and (0, 3), you would say "move forward 3 units while drawing, turn 90 degrees, move forward 3 units while drawing, turn 90 degrees, move forward 3 units while drawing, turn 90 degrees, move forward 3 units while drawing".
Obviously that's a lot of text, so each command is represented by a single character:
- + = Turn left
- - = Turn right
- ^ = Pitch up
- & = Pitch down
- \ = Roll counter-clockwise
- / = Roll clockwise
- | = Turn around
- F = Move forward while drawing
- f = Move forward without drawing
- [ = Save current position and orientation
- ] = Restore saved position and orientation
The rotation commands all rotate the same amount, which is determined when the turtle is initialized. The same goes for the distance the movement commands travel.
If we were to create the same square as before using actual Turtle Graphics commands:
Rotation: 90 degrees
Movement: 3 units
Commands: F+F+F+F
How does this relate to L-Systems?
The turtle receives its commands in the form of a string of characters. Any characters which are not one of the commands are simply ignored. This means that we can use L-Systems to generate strings containing Turtle Graphics commands!
Sounds cool, I want to use these in Dynamo!
Great, because I created a Turtle Graphics package that's available for download via the Dynamo Package Manager!
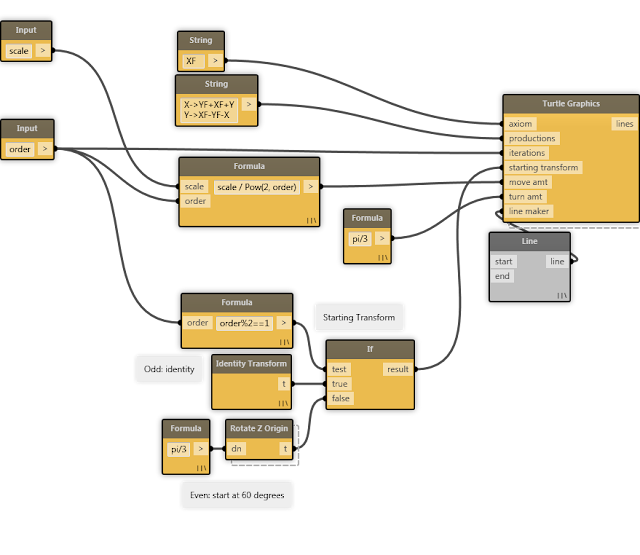
The main interface that the package provides is the Turtle Graphics node:
- start: The axiom of the L-System
- rules: Productions for the L-System
- iterations: Number of times to apply the productions to the L-system product
- initial transform: Starting transformation for the turtle
- move amt: Amount the turtle will move during the F and f commands.
- turn amt: Amount the turtle will turn during the +, -, &, ^, \, and / commands.
- line maker: Function that consumes the two end points of a line drawn with the F command. This is used to generate the output of the Turtle Graphics node.
The Turtle Graphics node returns a list of all the lines it has drawn. In order to give the user some control over how lines are represented, I've provided the line maker input, which takes a function that will receive the two end points of a line, and what it produces will be stored in the final lines list that the node will output.
For simplicity, the rules port takes the productions as a string, consisting of a list of rules separated by newlines, each composed in the following format:
[x]->[rewrite string]
(Where x is a character, and rewrite string is the string of characters to replace x with.)
For simplicity, the rules port takes the productions as a string, consisting of a list of rules separated by newlines, each composed in the following format:
[x]->[rewrite string]
(Where x is a character, and rewrite string is the string of characters to replace x with.)
Example: Sierpiński Arrowhead
Productions:
X → YF+XF+Y
Y → XF−YF−X
We use the Line node as the line maker; for each line the turtle draws, Line will receive two end points (in the form of XYZs) and make a line object, which will be returned in the output list of the Turtle Graphics node.
(Note that you could use any node that can receive two XYZs in the place of the Line node, and it will change the data being output. You could, for example, plug in a List node with two input ports, and then the lines output of the Turtle Graphics node will return a list of lists that each contain two XYZs.)
 |
| "Sierpiński" example, order 8 |
Other Examples
Included in the Turtle Graphics package are examples of various L-Systems that you can use for reference.
 |
| "Plant" example, order 5 |
 |
| "Hilbert 3D" example, order 3 |


No comments:
Post a Comment